5Charlie CTF - Disorderly2
A write-up of the Disorderly2 crypto challenge from 5Charlie CTF.
Disorderly2
Disorderly2 - Challenge
It seems that Disorderly has been given a facelift. Use the attached script and some logic to break the cipher and get the flag.
Attachments:
ctlvoxqzgiaumcpuokwxuzbgmdxqaixdxgwufeojwqarvwckomvzgiaywhqtjcdplmdmowgajhpcwerfqgdxabpdvjzjvfqewreapqdjcdvlrowtcyzjczgljdicmzoarwcepmzmpambodcrduscerncphdojcdvkmwapxpcswyeuazjpdiareczonjdjslzmzjvszarioaugwxawtqkxigczmpzfydrwhfjtoawrwxkhozaxbwgusfjtdifjlctuwrfsgdytzaxvpbzjdmzrasuyozcvngxiagdvrvwapsyawkvjcqwxedgamtokazydgifxzcoxkwtcmdconxnpwvfoyatwuijqflzvywoyzrzxansmhtzsmbtofzjzmuzamcwsmczkhsjdanoyhcozjzfomazbpyadbtrnlaodrzyiawvygoadkrdqualyftezywjdotevcrehawmciqwxlwapjswbampfihzjozcghjwxqgczhnjgoadlrzlgcrzmswfrwychwjzestcmfwigvxuaozywciyzxiqagvdxfpvzxwxazquglyqndvgcxuzkfydgfmdflvqxdrkzsfuyqzuciprwridaokjipdquajqlcgzydxndcrqzarvplwcxgcwomwycpdiojofiugdyuzfejsgfzjwycpzmwqcrldapjazsjdjkpadxsfidugmzmvloadpxnuogwcrhldfrqczuijwmugdaskxqadbjtwalrifdxphwbrzywygauobmgeczycwnjawgorlwhcxvpqldamowanmqeavdjzcogjdmnawsxwgckxdmqtcvlzjcwpuqnyqzgfkxgnzargczjwxcwvygqczxdmbfdtoxotiwvarewvcrdpsajdxgcdywasnragzvxzpcujcsdbyhdfsmopedfmbzparpaedjpiwvydxdrocjgzcvbrzclqbxowkgaujszaxblfwqxbgzjdmqznaejtihswcxdcstexdalvjdywghcmtbwfjzqcjczqgujzxbszaycezuqrwmtzauyfizgyqdfrswatvyocvbezypkzcjnzcysazgjilfguoyzfuktqrhanzpqrehadmatndjgwcjqickthjsfziyldohayophcblrdvatmqfdnrhztnfmfowxcbwtjgdbcxlbqwcynaqlvgrawobmbwavgjqnkcphyangzqumvkzaxtfzrtfsdykdchxfbgkvsjewpamfzbjecwhrgnhoazrkotwfyhcwtsjcnzjqlghbaxzsfpjdncvprlczgyeavzywihqgfxlczrdnceqjtikwcsm
...
bits = {
64: alphabet[0:3],
32: alphabet[3:6],
16: alphabet[6:9],
8: alphabet[9:12],
4: alphabet[12:15],
2: alphabet[15:18],
1: alphabet[18:21],
}
endbit = alphabet[21:26]
...
for bit in bits.keys():
if ord(letter) & bit:
crypt_letter += choice(bits[bit])
crypt_letter = list(crypt_letter)
shuffle(crypt_letter)
...
Disorderly2 - Solution 1
Code: https://gist.github.com/cetaSYN/2f6fe2048202104bf7eb8be859dc0ca5
I started my solve by pouring over the code and ensuring I understood exactly what was happening. The code takes a string and converts each character into it’s binary representation. The “on” bits are then converted to a letter of the alphabet that is within a group of letters representing that bit-power. There are 7 sets of 3-letter groups and an 8th set of 5 letters representing delimiters. This would be fairly strightforward except the generated representation is shuffled and the alphabet used to encrypt is also shuffled.
I decided to solve the Bonus first, which showed me that brute forcing it was not a reasonable approach. After a little fumbling with frequency analysis, etc, I reasoned that I could figure out the delimiters by hand.
I was able to recover the delimiter characters by detemining which characters were never seen directly adjacent to eachother. Every letter required at least one “on” bit, so every delimiter would have at least one separating character. I initially tried using the most frequent characters, but determined that wasn’t working (the most frequent would be 64 and 32 bitfields, not delimiters). I ended up stepping loading up the string in VSCode (as shown below) and stepping out ~3-5 characters (assuming that was the most common lengths) using the the Find feature, and seeing if the highlighting was adjancent. It was a bit of manual work, but ended up working out.

We now had our delimiters: jmrxy
Finding the delimiters cut a big chunk out of the “keyspace”, bringing it down to only 182.5 trillion possible combinations. That’s still not a reasonable brute, so more hand-solving was needed.
I looked at how all the characters were represented in binary…
...
01111000 - x
01111001 - y
01111010 - z
00100000 - [space]
01011111 - _
...
The space character only contains a single “on” bit, which means it will only be represented by a single letter.
After eliminating the delimiters, I was able to determine how the encoded data aligned to words AND which characters represented the 2^6 (64) field: acf
137 billion possible options left, but we now have our data split into words. Looking at the data, I notice most of the segments appear to be the length of normal English words with the exception of the final segment. I figure that’s our flag.
01100110 - f
01101100 - l
01100001 - a
01100111 - g
01111011 - {
Splitting that section out visually, I was able to verify my hunch about the the last segment starting with “flag{“. From there I was able to eliminate the known 64-bitfield and determine several other fields based upon repeated “on” bits and repeated letters.
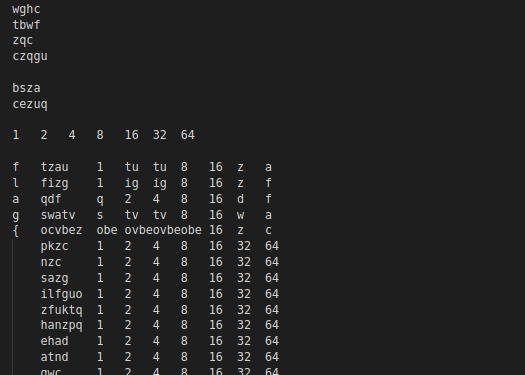
A bit more fiddling and I had solved the following:
Delim jmrxy
64 acf
32 dwz
1 oqs
This brings us down to (12!) / (3!3!3!3!) or 369600 possible combinations.
This is now well within the realm of brute-forcing, and I’m lazy.
...
def alphagen():
# Generate all possible usable alpabets
ALPHABET = list("beghiklnptuv") # Removed known
a0 = ["x", "y", "m", "j", "r"] # Delim
a1 = ["f", "c", "a"] # 64
a2 = ["w", "d", "z"] # 32
a3_sub = [c for c in ALPHABET if c not in a2]
for a3 in list(itertools.combinations(a3_sub, 3)): # 16
a4_sub = [c for c in a3_sub if c not in a3]
for a4 in list(itertools.combinations(a4_sub, 3)): # 8
a5_sub = [c for c in a4_sub if c not in a4]
for a5 in list(itertools.combinations(a5_sub, 3)): # 4
a6_sub = [c for c in a5_sub if c not in a5]
for a6 in list(itertools.combinations(a6_sub, 3)): # 2
a7_sub = [c for c in a6_sub if c not in a6]
a7 = ("s", "o", "q") # 1
yield "".join(
list(itertools.chain(*[a1, a2, a3, a4, a5, a6, a7, a0]))
)
def do_work(alphabet):
decmsg = decrypt(encmsg, alphabet)
if re.search(FLAG_PTRN, decmsg) and "congratulations" in decmsg.lower():
print("FOUND: {}\nABET: {}".format(decmsg, alphabet))
with Pool(6) as pool: # 6-core multiprocessing pool
pool.map(do_work, alphagen()) # Distribute work across cores
Wow. I wasn't even sure that Disorderly 1 could be solved. Congratulations! I'm basically just writing out a bunch of words so you have more data to work with. Otherwise it would be more difficult. Anyway, your flag is flag{the_world_is_finally_in_order_through_entropy}
ABET: fcawdzeklbingpthuvsoqxymjr
Flag: flag{the_world_is_finally_in_order_through_entropy}
Disorderly2 - Solution 2
Code: https://gist.github.com/cetaSYN/c7c6050ff141a02062598095254fbf22
After initially solving the challenge I talked through my method with the challenge designer and he raised an alternative method that I will be using here. At this point I had determined I didn’t have enough free time to participate competitively anymore, so I opted to re-solve Disorderly in a cleaner method and give myself a refresher in C.
The concept is straightforward: There is only one character per segment representing an “on” bitfield. This means that we will never see two characters together in a segment that represent the same field. By splitting the challenge into it’s segments/character-representative strings, and determining which characters are never seen together, we can conclude that those characters belong to the same bitfield.
#include <errno.h>
#include <stdio.h>
#include <string.h>
#include <sys/stat.h>
#include <sys/types.h>
#define FILE_BUF_SZ 2048
#define ABET_LEN 26
#define DELIM_LEN 5
#define ALPHA_START 97
/**
* Print usage message to stderr
*/
void print_usage(char* path)
{
fprintf(stderr, "Usage: %s <delimiters{5}> <path>\nExample: %s vwxyz ./message.txt\n",
path,
path);
}
/**
* Alters a letter buffer to set a specified character to space
*/
void lbuf_spc_char(char* letter_buf, char c)
{
char* c_loc = strchr(letter_buf, c);
if (c_loc) {
*c_loc = ' ';
}
}
/**
* Returns non-space character count until \0
*/
unsigned int nonspc_strcnt(char* str) {
unsigned int count = 0;
while(*str) {
if(*str != ' ') {
count++;
}
str++;
}
return count;
}
/**
* Prints a string while removing all spaces
*/
void nonspc_print(char* str) {
while(*str) {
if(*str != ' ') {
putc(*str, stdout);
}
str++;
}
}
int main(int argc, char* argv[])
{
if (argc != 3) { // Verify correct number of args
print_usage(argv[0]);
return -1;
}
if (strlen(argv[1]) != DELIM_LEN) { // Verify correct delimiter string length
fprintf(stderr, "%i delimiters characters required\n", DELIM_LEN);
print_usage(argv[0]);
return -1;
}
FILE* f = fopen(argv[2], "r"); // File pointer
if (!f) { // Verify successful file open
int err = errno;
fprintf(stderr, "Failed to open: %s - %s\n", argv[2], strerror(err));
return -1;
}
char bits_delim[6] = { 0 }; // Delimiter bits
strncpy(bits_delim, argv[1], DELIM_LEN);
char contentbuf[FILE_BUF_SZ]; // Encoded text file content buffer
fscanf(f, "%s\n", contentbuf); // Read file contents
// Create and fill alphabet letter solve buffers
char letters_buf[ABET_LEN][ABET_LEN + 1];
for (int a = 0; a < ABET_LEN; a++) {
strcpy(letters_buf[a], "abcdefghijklmnopqrstuvwxyz\0");
}
// Pre-remove delimiters
for (int a = 0; a < ABET_LEN; a++) {
for (int dc = 0; dc < DELIM_LEN; dc++) {
lbuf_spc_char(letters_buf[a], bits_delim[dc]);
}
}
char* token; // Pointer to representation of encoded character
char* psub = contentbuf; // Pointer to delimiter position in content buffer
// Iterate over delimiters
for (;; psub = NULL) {
token = strtok(psub, bits_delim);
if (token == NULL) {
break;
}
// Iterate over characters in token - index of letter_buf
int tok_len = strlen(token);
for (int i_lb = 0; i_lb < tok_len; i_lb++) {
// Iterate again, remove all other characters from representative array
for (int i_c = 0; i_c < tok_len; i_c++) {
if (i_lb == i_c) {
continue; // Don't remove self
}
lbuf_spc_char(
letters_buf[(*(token + i_lb) - ALPHA_START)], // Index of letter buf by iter position offset
*(token + i_c)); // Letter by iter position offset
}
}
}
// Print sets of 3
for (int a = 0; a < ABET_LEN; a++) {
if (nonspc_strcnt(letters_buf[a]) == 3) {
nonspc_print(letters_buf[a]);
printf("\n");
}
}
fclose(f);
return 0;
}
Unfortunately it doesn’t tell use what the value of the bitfields is though, so we would need to either do some intelligent solving on that or brute it, of which I opted for the latter.
...
def alphagen(sets, delims):
for i in list(itertools.permutations(sets, 7)): # Generate all possible sets
yield "".join(
# Combine tuples and append delimiters
list(itertools.chain(*[i[0], i[1], i[2], i[3], i[4], i[5], i[6], delims]))
)
def main():
parser = argparse.ArgumentParser()
parser.add_argument("delimiters")
args = parser.parse_args()
if len(args.delimiters) != 5:
raise Exception("Must specify all 5 delimiter characters as a single string")
# Get and handle set solving from binary
sets = (
subprocess.check_output(["./setsolve", args.delimiters, "encoded.txt"])
.decode()
.split("\n")
)
sets = [s for s in list(set(sets)) if s != ""] # De-duplicate and remove empty
for alphabet in alphagen(sets, args.delimiters): # Iterate over all possible alphabets
decmsg = decrypt(encmsg, alphabet)
if re.search(FLAG_PTRN, decmsg):
print("FOUND: {}\nABET: {}".format(decmsg, alphabet))
break
...
I still opted to figure out the delimiters by hand, so I passed those in as an argument.
$ gcc -Wall -pedantic -o setsolve setsolve.c
$ python3 c_solve.py jmrxy
Wow. I wasn't even sure that Disorderly 1 could be solved. Congratulations! I'm basically just writing out a bunch of words so you have more data to work with. Otherwise it would be more difficult. Anyway, your flag is flag{the_world_is_finally_in_order_through_entropy}
ABET: fcawdzeklbingpthuvsoqxymjr
Flag: flag{the_world_is_finally_in_order_through_entropy}
Disorderly2 (Bonus)
Disorderly2 (Bonus) - Challenge
How many effective alphabets are possible using disorderly2.py? Free hint: it’s not 26 factorial
Disorderly2 (Bonus) - Solution
I’m not great with math but enough fumbling around on Google gets you to the formula:
(n!) / (n₁!n₂!n₃!...)
Which becomes:
(26!) / (3!3!3!3!3!3!3!5!)
Flag: 12005466163891200000
This number isn’t nearly as high as the hint-negated 26!, but is still provided to show that raw brute force isn’t a feasible approach.
